2025年10月2日 掲載

物価上昇続く日本

長く続いた物価安定の時代が終わりを告げ、現在の日本では年間2〜3%の物価上昇が続いている。総務省統計局の消費者物価指数によると、2020年を100とした場合、2025年5月には111.8と約12%上昇し、特に食料品に限ると24.4％もの上昇を示している。消費者物価は数多い経済統計の中でも、特にその重要性が際立っている。しかし、公表されている物価指数が、私たちが日々直面する「物価」の変動を正確に反映しているのかという疑問の声も少なくない¹。

オタワ会議とスキャナーデータの登場

物価指数計測に関して、国連統計委員会によって1994年に設置された専門家会合がある。これは「オタワ会議」と呼ばれ、2年に一度、全世界の物価指数作成担当者や学術研究者が集まり物価計測に関するさまざまな問題を議論している。

前回のオタワ会議は、創設30周年記念大会として2024年に開催された。そこでは長年物価計測研究を牽引してきたアーウィン・ディーワート（Erwin Diewert）氏が記念講演を行い、特に「スキャナーデータ」に関して語っていた²。スキャナーデータとは、店舗のレジにおける売上データを集計したもので、Point of Sales（POS）データとも呼ばれる。これはいわゆるビッグデータの代表格であり、物価に限らず、近年、経済学やマーケティング等、多くの研究で用いられている。

スキャナーデータが物価計測に用いられ始めたのは、約30年前の第1回オタワ会議の頃であった。ディーワート氏は、初めてスキャナーデータに触れた際の衝撃を振り返り、「これで物価計測の深刻な問題は解消される」と感じたと語っていた。

しかし、実際には、物価計測にひそむ深刻な問題を浮き彫りにしたのであったと彼は続けた。スキャナーデータは確かに膨大な情報量を有するが、それによって、従来の手法では見えなかった経済計測上の重要かつ深刻な課題が明らかになったのである。ディーワート氏がその講演で強調したのは、指数理論における「連鎖ドリフト」と呼ばれる問題である。この連鎖ドリフトは、この15年以上、物価指数作成の現場と学術研究において中心的な課題となっている。連鎖ドリフトは100年以上前から知られていたが、多くの研究者はそれが深刻な問題であるとは考えていなかったのである。本稿では、スキャナーデータが明らかにした連鎖ドリフトの問題について紹介する。

物価計測方法

スキャナーデータを用いない場合、各国の物価は、各商品グループで代表的な商品を一つか複数選び、その価格を追跡調査して計算される。たとえばアイスクリームであれば、ハーゲンダッツ・バニラ（110mlカップ）である。日本では、各地域で、代表的と見なされるある特定店舗におけるハーゲンダッツ・バニラの価格をもって、その地域すべてのアイスクリーム（シャーベットやソフトクリームを含む）を代表させるのである。この手法に対しては、以下の問題点を指摘できる。（1）果たしてハーゲンダッツ・バニラだけでアイスクリーム全体を代表できるのか、（2）通常価格のみで特売価格を排除することで失われる情報はないか、（3）大規模店舗のみで物価は測れるのか³、（4）ハーゲンダッツ・バニラがどの程度販売されているか、という数量情報が不要なのか等である⁴。これは、統計調査員を用いる人力調査の限界でもある。一方、多くの店舗でのレジにおける取引情報に基づくスキャナーデータは、以上の問題に対してほぼ完全な解決策を提示する。そこでは店舗単位ではほぼすべての商品、ハーゲンダッツ・バニラだけでなくすべてのアイスクリームやシャーベットの、特売を含むすべての商品の価格が、数量と共に記録されるためである。スキャナーデータにより、物価計測に新たな時代が到来する、と多くの研究者が考えたのは自然なことである。

商品の移り変わりと連鎖指数

しかし、ディーワート氏が指摘するように、実際にスキャナーデータを用いて品目単位の物価指数を計算しようとすると、直ちに深刻な問題に直面する。アイスクリームを例にとると、毎年新しいアイスクリームが市場に投入される。そのような新しい商品は、既存のアイスクリームと比較して値上げされているのか、それとも値下げになってるのだろうか？ハーゲンダッツ・バニラだけを調べるのであれば、たとえハーゲンダッツ・バニラがリニューアルされたとしても、容量の変化をみれば、それが値上げか値下げのどちらかは分かりやすい。しかし、数百、数千種類にのぼるさまざまなアイスクリームやシャーベットで、全く新しい風味や形状の新商品が登場したら、それが値上げか、あるいは値下げかを判断することは非常に困難であり、そもそも統計担当者の主観に依存する手法は、その根拠があいまいになるなどの多くの問題がある。

オーストラリアなど、スキャナーデータを用いて日用品の物価を計測する国では、2時点間で同時に存在する商品価格のみを用いている。こうすれば、新旧商品の品質の違いを考慮する必要がなくなる。しかし、たとえば洗剤のような商品では、数年間でほとんどの商品が入れ替わってしまうため、2時点間が極力短い間、通常は1か月間の物価比較を行い、それを積み上げて長期的な物価を計算する、という連鎖指数と呼ばれる手法を用いている。

連鎖指数は、1887年に、著名な経済学者であるアルフレッド・マーシャルが、商品が入れ替わっていくことによる物価計測上の問題を緩和するために提唱した手法である。たとえば2020年と2023年の物価を比較するとしよう。伝統的な手法では、2020年における商品価格を2023年の商品価格と比較することになる。したがって、2020年に存在していた商品が2023年に存在しなかったら物価を計算することができない。しかし、2020年と2021年の比較をするのであれば、1年間生き残っている商品は多いだろう。そこで、まず2020年と2021年の物価を、両時点で共通する商品に限定して計算するのである。そうして得られた物価指数をP(2020, 2021)と書くことにしよう。次に、2021年と2022年の間の物価、P(2021, 2022)を計算し、さらに2022年と2023年の物価、P(2022, 2023)を計算する。そして、2020年から2023年の間の連鎖物価指数（Chain Price Index）、P^c(2020,2023)を

と定義するのである。すなわち、長期的な物価は、毎年の物価の積み上げの結果だと見なすのである。

一般にP^c (2020,2023)≠ P(2020,2023)、すなわち、3年前の商品価格を直接比較して計算する標準の物価指数と毎年の物価を積み上げる連鎖の物価指数は一致しない。たとえば、3年前と現在で共通商品が存在しなかったら、そもそも右辺は計算できない。この二つの指数の差が連鎖ドリフトと呼ばれるものである⁵。

実際に、洗剤のスキャナーデータで連鎖指数を計算してみよう。図1はインテージ社が提供する、1000店舗を超える大規模なスキャナーデータを使って、消費者物価指数の算式として広く用いられているラスパイレス指数について、連鎖指数と基準時の商品価格を直接比較する伝統的な手法とを比較したものである⁶。基準時は2006年の第1週であり、赤線は毎週の物価指数を積み上げた連鎖指数、青線は2006年の第1週から直接各時点での商品価格を比較したものである。

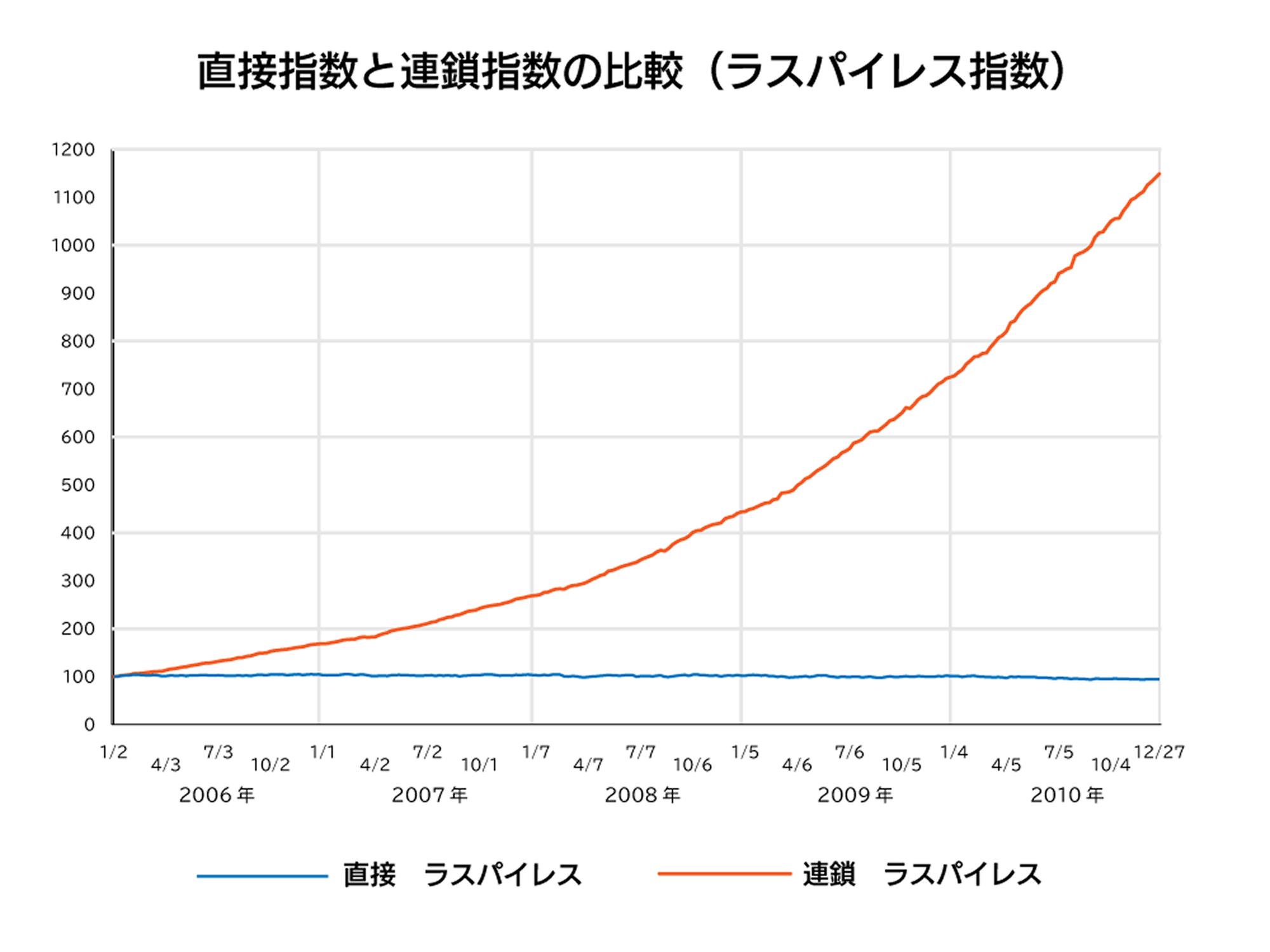
図1：直接指数と連鎖指数の比較（ラスパイレス指数）

縦軸の1000や1200という数値は物価指数であり、100であれば一定であることを意味する。すなわち、連鎖指数では、2010年の洗剤価格は2006年に比べて10倍以上になっていることになる。むろん、これは非現実的な値である⁷。一方、直接比較するラスパイレス指数は100程度で安定している。両者の差、すなわち、連鎖ドリフトが時間を通じて急拡大しているのである。

一方、国民経済計算で用いられるパーシェ指数を計算すると⁸、図2になる。データは図1と同じである。今度は、連鎖指数は急速にゼロに近くなっていく。すなわち、2006年に比較して、2009年ごろは、洗剤の価格はほぼゼロになっていることを意味する。それに比べ、直接2006年の商品価格と比較する直接指数では、パーシェ指数は100前後で安定している。すなわち、こちらも連鎖ドリフトが急拡大している。ラスパイレス、パーシェのどちらも、連鎖指数はこのままでは使い物にならないのである⁹。この急拡大する連鎖ドリフトこそ、オタワ会議30周年記念講演でディーワート氏が指摘したスキャナーデータ活用の大問題なのである。

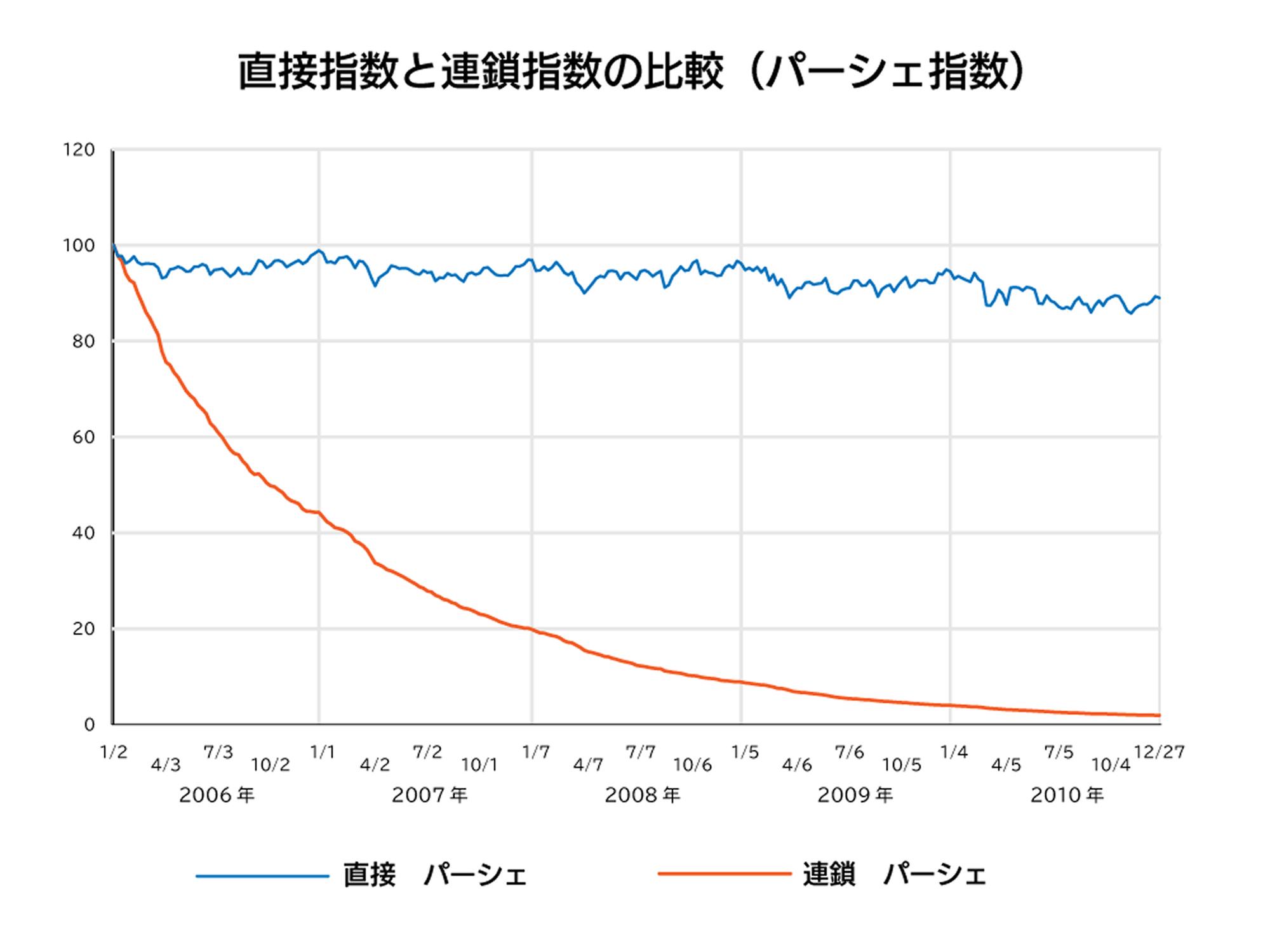
図2：直接指数と連鎖指数の比較（パーシェ指数）

連鎖指数がそのままでは使い物にならない一方、直接指数は、商品が入れ替わってしまい、洗剤に関しては、5年以上もの間継続して販売されている商品は1%程度しかない。そのごくわずかな商品の情報に基づくことになるために、こちらも信頼性に疑問が生じてしまう。

連鎖ドリフトの存在そのものは昔から知られており、解決方法として、コンラッド・ジニが1931年に提唱した手法が、現在オーストラリア統計局で用いられている。これはテクニカルなので詳細は省くが、連続する2時点だけでなく、すべての時点間の物価指数を計算して、膨大な数の連鎖指数を割り出し、その平均を用いることにより強引に平滑化させるものである。これにより、形式的には安定した物価指数が得られる。また、この手法は世界銀行が購買力平価を計算する際にも使用されている。しかし、残念ながらこの手法にも、現在の物価上昇を把握するには深刻な問題が存在する。

たとえば、ある商品の値上げが、その商品の価格変更ではなく、商品に含まれる量を減らす「シュリンクフレーション」と呼ばれる実質値上げによって行われたとしよう。牛乳が1000mlから900mlに減ったような場合である。容量が減った商品は、旧商品とは異なる商品となるため、その商品が登場し、旧商品が消滅した時点では、新たな商品と旧商品の価格は比較できず、物価指数には反映されない。物価指数に反映されるのは、新商品が登場した次の時点からである。これは、連鎖指数を用いた場合、容量調整による実質値上げを反映しないことを意味する。シュリンクフレーションは日本のみならず欧米でも観察されている。しかし、スキャナーデータを活用し、2時点のどちらにも存在する共通商品に限定した物価指数では、それを把握できないのである。

連鎖指数では、新商品登場時の実質値上げを把握できないだけでなく、商品が消える際の問題も把握できない。たとえば、非常に人気のある商品がなくなり、後継商品もないとしよう。このとき、人々の経済厚生は低下するだろう。しかし、現在作成されている物価指数は、その時点に存在する商品の価格しか反映しないため、商品が消滅してもその情報は無視されてしまうのである。商品の消滅の影響は、たとえばコロナ禍で海外旅行やスポーツ観戦といった商品がなくなったときに、それをどう物価に反映させるべきかという激しい論争が物価研究者の間で繰り広げられた。筆者もその論争の当事者の一人であるが、これは現在でも結論が得られていない¹⁰。

スキャナーデータという多くの商品情報が含まれるデータを用いることで、商品の消滅と生成が持つ経済的含意の重要性が、物価計測担当者と研究者に突きつけられたのである。

新しい物価指数の模索

現在、筆者を含む多くの研究者は、スキャナーデータに基づき、商品の生成・消滅を適切に反映する物価指数の構築に取り組んでいる。

一つの方向性は、経済理論を用いることである。家計の効用最大化問題を前面に出し、商品の消滅と生成が家計の厚生にどのような影響を与えるかについてを経済モデルで推計し、それを反映した消費者物価を計測するのである。効用関数に強い仮定を置く必要はあるものの、分析そのものは伝統的なミクロ経済学のモデルとほぼ同じフレームワークで行うことができるので、経済学者の多くはこの手法を採用している。

第二の方向性は、統計モデルを駆使するものである。まず、さまざまな商品価格の共通変動を物価として定義する。次に、各商品価格を商品属性の関数と見なし、そこから連立方程式を導き、システム推計から機械的に物価を計算するのである。これはタイムダミー変数を用いたヘドニック手法であり、テレビやパソコン、デジタルカメラなど、耐久消費財の一部ですでに消費者物価指数として採用されているが、それをより広い商品に拡大するのである。

前者は経済理論に即しており、その結果に明快かつ経済学的な解釈を与えることが可能である。しかし、効用関数の仮定に全面的に依拠してしまうため、日々の統計作成業務に応用することは困難であろう。特に経済学者でないものにとっては、効用関数と最適化行動の仮定に依拠するこの手法はなかなか受け入れることが難しいだろう。一方、後者はデータを基に機械的に計算するため公的統計に用いる際には適しているが、商品属性の情報が限られていると統計モデルの信頼性に疑問が生じてしまうし、得られた物価統計の解釈が明確にならない、という欠点がある。

近年では、経済理論に即してはいても、「商品」から効用を得る、という伝統的な立場ではなく、商品の「機能」から効用を得る、という考え方に基づき、統計モデルと経済モデルの融合を進めるアプローチが登場している¹¹。たとえば、私たちがコンピューターを購入するのは、コンピューターそのものから効用を得ているのではなく、コンピューターが提供する、検索や作文する機能から効用を得ているのであり、同一の機能を提供する二つのコンピューターは、たとえ異なる商品であっても実質的に同一のコンピューターと見なすのである。そして、商品がどんなに入れ替わっても、提供する機能が同一であれば、それは商品の入れ替わりとは見なさいのである。筆者は両方の手法で研究を進めているが、どちらも一長一短であり、まだ決め手は見つかっていない。前者はより経済理論志向の強い研究者の間で、後者はより実務的視点の強い人たちの間で支持される傾向がある。だが、この分野の研究は急速に進んでおり、10年以内には、日本を含む各国のスキャナーデータを用いた物価計測の精度は飛躍的に向上すると期待されている。

¹日本銀行が四半期ごとに行っている『生活意識に関するアンケート調査』によると、人々の認識する物価上昇は、消費者物価指数が示す値よりもはるかに大きな値になっている。

²ディーワート氏の報告の元となった原稿は
https://stats.unece.org/ottawagroup/download/slides-diewert-on-the-ottawa-group-after-30-years.pdf
からアクセス可能である。

³大規模店舗に限定すると、多くの場合コンビニエンスストアの価格動向を無視することになってしまう。

⁴たとえば、東日本大震災は2011年3月11日に生じたが、その時までには3月の価格調査のほとんどは終わっており、次の価格調査は翌月の4月中旬となる。すなわち、震災が短期的にどのような影響を物価に与えたか、消費者物価指数からは分からないのである。

⁵連鎖ドリフトに関しては理論的な研究が多く発表されている。詳細は、阿部（2023）、Abe（2025）を参照されたい。

⁶ラスパイレス指数は世界各国の消費者物価指数として採用されているものであり、基準時のさまざまな商品の数量を、比較時点で購入したらどの程度支出額が増加（減少）するかを示す。

⁷図1および図2に関しては阿部（2023）およびAbe（2025）の第8章に詳細な説明がある。

⁸パーシェ指数は、比較時のさまざまな商品の数量を、基準時点で購入したらどの程度支出額が増加（減少）するかを示すものであり、国内総生産の推計で用いられている。

⁹ラスパイレス指数とパーシェ指数の幾何平均であるフィッシャー指数を用いると、上昇と下落が打ち消しあい、連鎖ドリフトは減少するが、それでも非現実的な大きさの連鎖ドリフトが生じてしまう。詳しくは阿部（2023）、Abe（2025）を参照されたい。

¹⁰コロナ禍における商品の消滅と物価計測の論争に関心がある方は、2022年のJournal of Official Statistics,38(1)がその問題に関する特集号であり、ディーワート氏と筆者を含む複数の研究者のコメントが掲載されているので参照されたい。

¹¹代表的な研究はCrawford and Neary（2023）である。