精度保証付き数値計算と水面波方程式
- 商学研究科准教授小林 健太
2015年冬号vol.45 掲載
コンピュータを利用した数学的証明
数学の証明というと、紙と鉛筆で地道にやるものというイメージが強いかもしれませんが、近年、数学的証明へのコンピュータの利用が広がってきています。4色定理(いかなる地図も、4色あれば、隣り合う領域が異なる色になるように塗り分けられるという定理)がコンピュータによって証明されたことは有名ですが、その他にも、ケプラー予想(空間に球を詰める最も効率の良い方法についての予想)や、カオスの存在証明など、重要な問題がコンピュータによって証明されています(他にもさまざまな例があります)。
筆者は以前から、コンピュータを用いた数学的証明の理論である精度保証付き数値計算に関する研究を行っており、2014年には、水面波方程式への応用についての研究が評価され、精度保証付き数値計算に関する国際的な賞であるR.E.Moore Prizeを授与されました。本稿では、受賞対象となった研究についてご紹介したいと思います。
水面波方程式

図1
青海波

図2
富嶽三十六景(神奈川沖浪裏)
古くから洋の東西を問わず、人間は水面に生じる波、いわゆる水面波に親しんできました。同時に、波の形についても興味を持っていたと考えられます。図1は青海波と呼ばれる日本の文様ですが、丸い波の形が見られます。この文様は、一説によると、シルクロードを通じて中国の西域から伝わったといわれています。図2は葛飾北斎の有名な浮世絵ですが、鷹の爪のような複雑な形状が描かれています。この作品はヨーロッパに伝わり、ゴッホなどに影響を与えたといわれています。波の形状についての興味が普遍的であることを示す好例といえるでしょう。

図3
北海道・然別湖で筆者撮影
水面波に関する科学的な研究は、18世紀になってオイラーとラグランジュが流体力学の基礎理論を構築してから始まりました。ただ、現実世界の水面波は、さまざまな要因が形成に影響し、極めて複雑な挙動を示しますので、そのままでは数学的な解析が難しいのが現状です(図3)。一般的に、実際の自然現象や社会現象は、さまざまな要因が複雑に絡み合って生じているため、そのままでは数学的な解析のベースには乗りません。そこで、まずは現象について、重要でないと思われる要因を除外したり、要因の影響の仕方をシンプルな関数で近似したり、などの単純化を行い、現象を表す方程式を作ることになります。
これを現象のモデル化といいます。このモデル化により、現象は偏微分方程式や常微分方程式、積分方程式などの方程式で表されることになります。私が研究対象とした方程式は、以下のような単純化によって得られます。
- 流体には通常、「粘性」つまり粘り気があります。しかし、水の粘性は非常に小さいので、考えないものとします(油などでは粘性は重要です)。
- 流体には通常、「圧縮性」という、圧力をかけると縮む性質がありますが、水の圧縮性は非常に小さいので、考えないものとします(気体では圧縮性は重要です)。
- 流体の運動は、「渦度」という、ある種の回転運動をする働きを含むことがありますが、ここでは渦度の無い動きを考えます。
- 津波のシミュレーションなど、3次元の波の数値計算などは広く行われていますが、数学的な解析はかなり難しいので、奥行き方向は形が変わらないものとして、2次元の問題を考えます。
以上の状況設定の下で、2次元非圧縮性流体に関するオイラー方程式※1と、表面張力と曲率の関係を表すヤング・ラプラス方程式※2により、水面波のモデル化が可能となります。
- 1:1755年にL.オイラーにより定式化された流体力学の基礎方程式。L.オイラー(1707-1783)は数学・物理・天文学などの分野に莫大な業績を残した巨人ともいわれる人物。
- 2:液体と気体の境界(界面)に生じる圧力差についての方程式。T.ヤング(1773-1829)はイギリスの物理学者で、弾性体力学の定数ヤング率に名前を残している。P.S.ラプラス(1749-1827)はフランスの科学者で、自然科学、数学、物理学、天文学などに広く業績を残している。
ネクラソフ方程式とストークス極限波
水深が波の波長に比べて浅い場合には、さらに近似を入れることにより、ブシネスク方程式※3、KdV方程式※4などの波の方程式が得られます。一方で、水深が無限に深く、波の形が周期的になっているような状況を考えると、レヴィ・チビタ方程式※5が得られます。レヴィ・チビタ方程式は、重力や表面張力の影響を考慮した方程式となっていますが、波のスケールが数m以上になると、重力の影響に比べて表面張力の影響は非常に小さくなることが知られています。そこで、さらに表面張力の影響を無視して得られるのがネクラソフ方程式※6です。
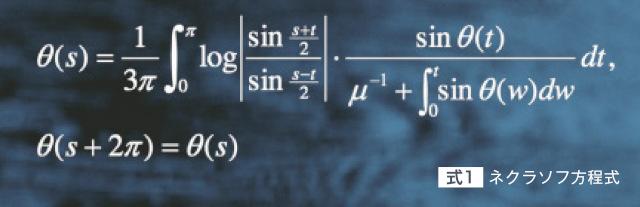

ネクラソフ方程式を式1に示します。ここで、sは水面を表すパラメータで、2πが波長の一周期に対応します。また、θ(s)はsにおける波面と水平面のなす角を表します。µは、波の波長、速度、重力加速度により決まる定数です。ネクラソフ方程式の解としてθ(s)が求められれば、波の形状は式2により求めることができます。ここで、Hはヒルベルト変換※7(ある種の積分変換)です。
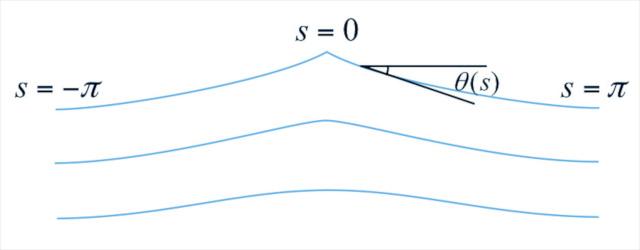
図4
ネクラソフ方程式から計算した水面波
ここからは、一周期に山と谷が一つずつあるような波を考えましょう。図4に、いくつかのµ に対応する水面波の一周期の形状を示します。µが大きくなればなるほど波の頂点における曲率が大きくなり、µ が無限大のときには波頭の尖った波になります。この波を、ストークス極限波※8といいます。
ここからは特に、ストークス極限波について考えます。µ が無限大のときにネクラソフ方程式に解が存在する、つまりストークス極限波が存在するということは1978年にJ.F.トーランドにより証明されましたが、取りうる波形が一つしかないか、もしくは複数あるかという問題は長らく未解決でした。
- 3:浅い水の上の波を表す方程式。J.V.ブシネスク(1842-1929)はフランスの数学者、物理学者。
- 4:浅い水の上の孤立波を表す方程式で、可積分系といわれる分野の発展のきっかけとなった方程式。方程式の名は、研究を行ったD.コルトヴェーグ(1848-1941)とG. de フリース(1866-1934)にちなむ。
- 5:深い水の上の周期的な波の方程式。T.レヴィ・チビタ(1873-1941)はイタリアの数学者で、解析学の分野で活躍。
- 6:重力のみを外力とする周期的な水面波についての方程式。A.I.ネクラソフ(1883-1957)はロシアの数学者。水面波の分野で多くの研究を行った。
- 7:信号処理や波動の解析などにしばしば現れる重要な積分変換。D.ヒルベルト(1862-1943)はドイツの数学者で、現代数学の方向性を指し示す指導的な数学者であったことから「現代数学の父」と呼ばれている。
- 8:G.G.ストークスによって発見された、水面波の極限形(いわゆる波頭の尖った波)。G.G.ストークスはアイルランドの数学者、物理学者で、流体力学、光学、数学などの分野で重要な研究を行った。
現実世界の現象と方程式
ここで、現実世界の現象とモデル化により得られた方程式の関係について説明しておきましょう。現実世界に水面波が存在するのだから、方程式の解としてストークス極限波が存在するのは当たり前だと思う人もいるかもしれません。しかし、現実の現象とそれをモデル化した数学の問題はイコールではないので、現象が存在したとしても、モデル化した方程式に解が存在するとは限りません。ただ、モデル化した方程式に、現象に対応する解が存在しない場合には、モデル化に何らかの不備がある可能性が高いといえます。一方で、モデル化により得られた方程式が現象を良く表している場合には、方程式の解の性質を調べることにより、現実に起きている現象の理解につながると期待できます。
解の性質のうち、特に重要なものが存在と一意性です。解が存在するかどうかは、実際の現象が存在するかどうかに関連しますので重要ですし、解が存在する場合、解が一つしかないのか複数あるのかも、現象が一通りに決まるのかどうかに関係しますので重要です。特に、ストークス極限波の一意性は、波頭の尖った波の形が一通りに決まるかどうかという問題に直結しており、古くから解決が望まれてきました。
ストークス予想
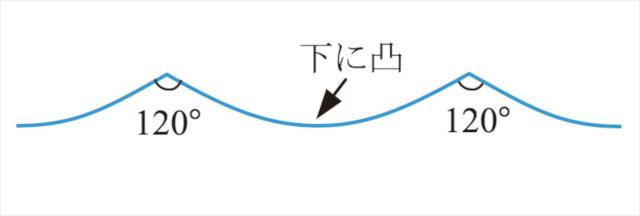
図5
ストークス予想
ストークス極限波の一意性は、ストークス予想という重要な予想との関連からも重要です。1880年にG.G.ストークスは、ストークス極限波について、ストークス予想といわれる次の二つの予想を提示しました(図5)。
- ストークス極限波の頂点は120度の角度をなす。
- 隣り合う2頂点の間では、波の波形は下に凸となる。
一つ目のストークス予想は1982年にC.J.エイミックらにより証明されました。しかし、二つ目のストークス予想は130年以上の間、未解決のままでした。2004年にはP.I.プロトニコフとJ.F.トーランドによって、頂点間の波形が下に凸となるようなストークス極限波が存在するということが証明されましたが、この結果は、二つ目の予想の完全な解決を意味しません。なぜなら、下に凸ではないようなストークス極限波が他に存在するかもしれないからです。しかし、もしストークス極限波の一意性が証明されれば、二つ目のストークス予想も完全に解決されることになります。
以上のような背景により、ストークス極限波の一意性は長らく懸案の問題だったのですが、筆者は2010年に、精度保証付き数値計算を用いてストークス極限波の一意性を証明することに成功しました。
不動点定理
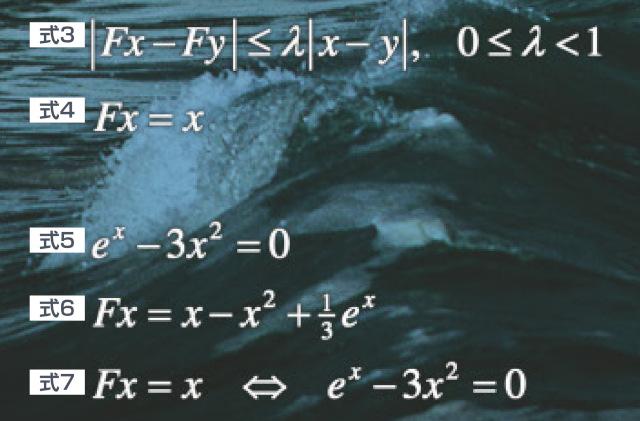
式3~7
イメージを掴んでもらうため、簡単な問題でバナッハの不動点定理の応用を説明しましょう。式5の方程式について、解が0.5〜1.0の間にただ一つ存在することを証明してみます。まず、写像Fを式6のように決めれば、式7が成り立ちます。つまり、元の方程式を不動点問題に書き換えることができます。さて、xとyを0.5以上1.0以下の相異なる数とすると、平均値の定理より、0.5以上1.0以下の数cが存在して式8が成り立ちます。よって式9のように変形するとバナッハの不動点定理の成立を示すことができ、式5の方程式が0.5〜1.0の間に解をただ一つだけ持つことが証明されます。この例においては、解は実数でしたが、数ではなく関数が解になる場合でも基本的な考え方は同じです。
不動点定理の条件は、Fの取り方にもよりますが、通常は解のごく近くの限られた領域においてでしか成立を証明できません。しかし、ストークス極限波については、すべての可能性を考えても解が一つしかない、いわゆる大域的な一意性を示さなければなりません。そのため、まずは解の存在範囲を限定された領域に絞り込み、その後に不動点定理の成立を証明しました。
- 9:写像の不動点に関する定理(不動点定理)の一つ。名称はS.バナフにちなむ。S.バナフ(1892-1945)はポーランドの数学者。現代的な解析学の構築において多大な貢献を行った。
一意性の証明のプロセス
それでは、私が用いた一意性の証明のプロセスについて概略を説明します。詳しく知りたい方は、論文1もしくはその要約版である論文2をご覧ください。
論文1
K. Kobayashi, On the global uniqueness ofStokes' wave of extreme form, IMA Journal ofApplied Mathematics,Vol.75[5] (2010), pp.647-675.
論文2
K. Kobayashi,Computer-AssistedUniqueness Proof for Stokes' Wave ofExtreme Form, NankaiSeries in Pure, AppliedMathematics andTheoretical Physics,Vol.10 (2013), pp.54-67.
まず、解くべき方程式を確認しておきます。

式8~11
ストークス極限波は、µ が無限大のときのネクラソフ方程式の解から得られますので、式10の解の一意性を示せばよいことになります。ここで、一周期に山と谷が一つずつしかないという条件から、sが0からπまでの間で正値を取るという条件が新たに加わっています。解の概形は図6のようになります。

図6
解の概形
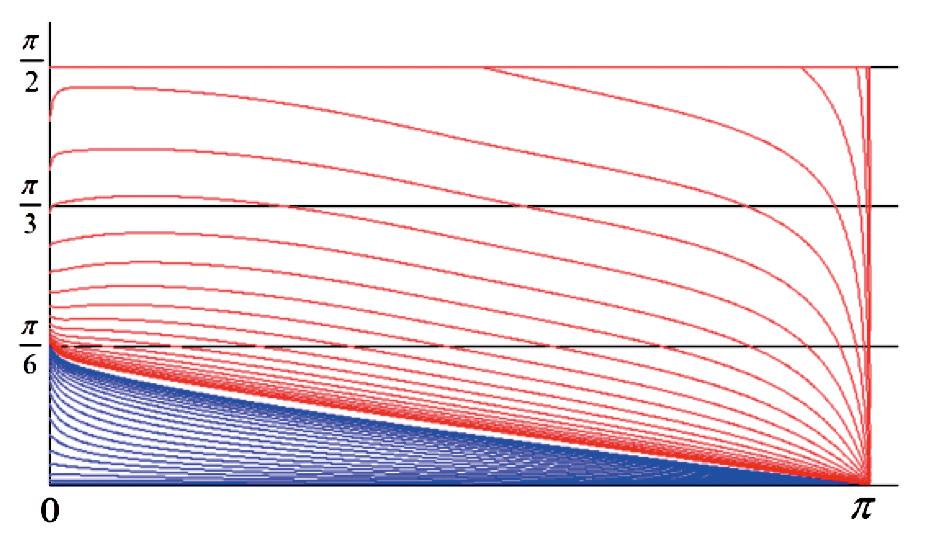
図7
解の範囲が絞り込まれる様子
式10の解θ(s)については、数学的な解析の結果として、式11に示すような上界関数と下界関数が知られています。この下界関数は筆者が求めたものです。さらに筆者は、
θ(s)の上界関数と下界関数から、より精度の良い上界関数と下界関数を計算する方法を開発しました。その方法を利用して、反復により解の範囲を絞り込んでいった様子が図7です。赤い線が上界関数を表し、青い線が下界関数を表します。反復とともに上界関数はより小さくなり、下界関数はより大きくなり、図7の段階では、解となる関数は、一番下にある赤い線(上界関数)と一番上にある青い線(下界関数)の間の細い領域だけに存在するということがわかります。
筆者は、このようにして解の存在する範囲を十分に絞り込んだ後に、不動点定理を適用し、解の一意性を証明しました。この証明のプロセスにおいては、解の絞り込みの段階で解の存在可能な範囲を限定し、その限定された領域において不動点定理を適用しているので、大域的な一意性が証明されていることになります。
精度保証付き数値計算
筆者の実際の証明にはコンピュータが多用されています。まず、上界関数と下界関数を求めるプロセスにおいては、それぞれの関数を区分的定数関数で評価して計算するということを行っています。その際、上界関数はより大きな区分的定数関数で上から評価し、下界関数はより小さな区分的定数関数で下から評価することにより、数学的に厳密な結果を得ています。通常、コンピュータによる計算では、実数を有限桁で打ち切ることによる丸め誤差が発生しますが、精度保証付き数値計算の一手法である区間演算という手法を用いることで、丸め誤差の大きさも厳密に評価しています。
不動点定理を適用する段階でもコンピュータを用いています。不動点定理の成立を示すには、式3に出てくる定数λの評価が必要になってきますが、今回の問題の場合、関数の入り組んだ非常に複雑な形について値を評価しなければなりません。紙と鉛筆でλを評価しようとすると非常な困難が予想されますが、筆者はこちらについても、出てくる関数たちをまず区分的定数関数で評価し、その上で区間演算を用いることでλの値が1未満であることを示すことができました。
まとめ
筆者の、精度保証付き数値計算を用いた研究により、何十年もの間、多くの研究者によって証明に向けて努力がなされてきたストークス極限波の大域的な一意性を、ついに証明することができました。この結果により、130年前に提示された重要な予想であるストークス予想の二つ目の予想が肯定的に解決されました。また、今回の成果は精度保証付き数値計算の分野でもインパクトがありました。精度保証付き数値計算を用いて方程式の解の局所的な一意性を証明した結果は多くありますが、解の大域的な一意性を証明した結果はほとんどありません。本研究はその非常に珍しい例となっています。今回の結果は、その結果自体も重要ですが、数学の証明におけるコンピュータ利用の可能性と将来性を示したという点においても、意義深いといえるでしょう。
(2015年1月 掲載)

